期权期货衍生品所需公式(期货期权及其衍生品)
将详细阐述期货、期权及其衍生品交易中常用的公式。期货和期权是金融市场中重要的衍生品,它们的价格波动受多种因素影响,而理解这些因素以及它们之间的关系需要运用一系列数学公式。这些公式不仅用于定价,也用于风险管理和策略制定。 将涵盖一些核心公式,并对它们的应用进行简要解释,但需要注意的是,实际应用中可能需要考虑更复杂的模型和因素。 掌握这些公式,有助于投资者更好地理解和参与期货和期权市场。
1. 期货合约价格计算
期货合约的价格并非随意设定,而是与标的资产的现货价格、时间价值以及融资成本等因素密切相关。 一个简单的期货价格模型考虑了现货价格、无风险利率和储存成本(或便利收益):
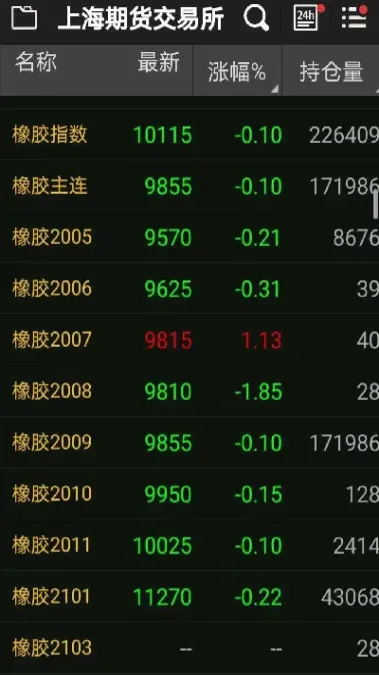
F = S e^(rT + c - b)
其中:
- F:期货合约价格
- S:标的资产现货价格
- r:无风险利率(年化)
- T:合约到期时间(以年为单位)
- c:储存成本(年化,例如仓储费),如果标的资产持有成本为负(例如,持有黄金的便利收益),则c为负值。
- b:便利收益(年化,例如,持有某种商品的便利收益),如果标的资产持有成本为正,则b为零。
- e:自然对数的底数 (约等于2.71828)
这个公式是一个简化模型,实际情况中,期货价格还会受到市场供需、预期等因素的影响,导致期货价格偏离理论价格。 例如,在供给短缺的情况下,期货价格可能高于理论价格;反之,则可能低于理论价格。
2. 期权定价模型 - 布莱克-斯科尔斯模型
布莱克-斯科尔斯模型 (Black-Scholes Model) 是期权定价中最著名的模型之一,它为欧式期权提供了一个理论价格。 该模型假设标的资产价格服从几何布朗运动,并考虑了无风险利率、波动率、到期时间和执行价格等因素:
C = S N(d1) - X e^(-rT) N(d2)
其中:
- C:欧式看涨期权价格
- S:标的资产现货价格
- X:期权执行价格
- r:无风险利率(年化)
- T:合约到期时间(以年为单位)
- σ:标的资产的波动率(年化)
- N(x):标准正态分布累积分布函数
- d1 = [ln(S/X) + (r + σ²/2)T] / (σ√T)
- d2 = d1 - σ√T
这个公式计算的是看涨期权的价格,对于看跌期权,公式略有不同。 布莱克-斯科尔斯模型的应用需要对标的资产的波动率进行估计,而波动率的估计本身就是一个复杂的问题。 该模型也基于一些简化的假设,例如不考虑股息、交易成本等因素,因此实际价格可能与模型计算结果存在偏差。
3. 期权希腊字母
期权的希腊字母是衡量期权价格对不同因素敏感度的指标,它们对于风险管理至关重要。 常用的希腊字母包括:
- Delta (Δ):期权价格相对于标的资产价格变化的敏感度。 Delta值介于0到1之间(看涨期权)或-1到0之间(看跌期权)。
- Gamma (Γ):Delta相对于标的资产价格变化的敏感度。 Gamma衡量Delta变化的速度。
- Vega (ν):期权价格相对于标的资产波动率变化的敏感度。
- Theta (Θ):期权价格相对于时间的变化率(时间衰减)。
- Rho (ρ):期权价格相对于无风险利率变化的敏感度。
理解这些希腊字母,可以帮助投资者更好地评估和管理期权交易的风险。 例如,高Delta的期权意味着价格波动较大,风险也较高;高Vega的期权对波动率变化非常敏感。
4. 期货和期权的套期保值
期货和期权可以用于套期保值,以降低价格波动带来的风险。 套期保值策略的具体公式取决于具体的风险和目标,但通常涉及到计算所需的头寸数量,以对冲潜在的风险。
例如,一个农产品生产商可以用期货合约来锁定未来的销售价格,从而避免价格下跌带来的损失。 计算所需的头寸数量通常需要考虑生产商的预期产量和期货合约的合约规模等因素。
5. 衍生品组合策略
投资者可以组合使用多种期货和期权合约来创造复杂的交易策略,例如:
- 牛市价差策略:买入低执行价格的期权,同时卖出高执行价格的期权,以获利于标的资产价格上涨。
- 熊市价差策略:买入高执行价格的期权,同时卖出低执行价格的期权,以获利于标的资产价格下跌。
- 跨式期权策略:同时买入看涨和看跌期权,以获利于标的资产价格大幅波动。
这些策略的盈亏取决于标的资产价格的走势,以及期权的执行价格、到期时间等因素。 计算这些策略的盈亏曲线需要用到期权定价模型和希腊字母等知识。
总而言之,期货和期权交易涉及到一系列复杂的公式和模型。 理解这些公式和模型对于投资者成功参与市场至关重要。 需要注意的是,这些公式和模型只是工具,实际交易中还需要考虑市场环境、风险管理等多种因素。 只是对常用公式的简要介绍,更深入的学习需要参考专业的金融教材和文献。