亚式期权名词解释(亚式期权名词解释是什么)
在金融衍生品的世界里,期权作为一种重要的工具,为投资者提供了对冲风险、套利以及进行投机的机会。传统的欧式和美式期权,其收益通常只取决于标的资产在特定时点(欧式)或期权生命周期内(美式)的价格。金融市场的复杂性和多样化的风险管理需求,催生了许多非标准期权,其中亚式期权(Asian Option)便是极具代表性的一种。亚式期权因其独特的收益计算方式——基于标的资产在一段时间内的平均价格——而备受关注。它有效平滑了短期价格波动带来的风险,使其成为特定场景下尤为有效的工具。
将深入探讨亚式期权的各项核心名词,从其基本概念、独特优势,到不同类型和定价考量,帮助读者全面理解这种独特的衍生品。
1. 什么是亚式期权?
亚式期权,顾名思义,是一种其支付(payoff)不依赖于标的资产在到期日单一价格点位,而是依赖于标的资产在期权存续期间某个特定观察期内的“平均价格”的期权。它属于路径依赖型(Path-Dependent)期权的一种,即期权的最终价值不仅取决于到期时的价格,还取决于标的资产价格在一段时间内的表现路径。与欧式期权只看“终点”不同,亚式期权更关注“旅途中的平均表现”。这种设计使得亚式期权在对冲那些长期或持续面临价格风险的头寸时,比传统期权更具优势。例如,一家航空公司购买燃油,其成本不是取决于某一天燃油的峰值价格,而是其长期采购的平均价格。在这种情况下,使用基于平均价格的亚式期权进行对冲,将更为精准和有效。
2. 亚式期权的核心特征与优势
亚式期权之所以在金融市场中占有一席之地,主要归因于其独特的核心特征和由此带来的显著优势:
1. 路径依赖性(Path Dependency):这是亚式期权最显著的特征。它的支付公式中包含了一个“平均值”项,这意味着在整个观察期内,标的资产的每个价格点都将影响期权的最终价值。这区别于传统期权,后者通常只关注到期日的最终结算价或行权价。
2. 降低波动风险(Reduced Volatility Risk):由于收益是基于平均价格计算的,因此短期内标的资产价格的剧烈波动对其最终收益的影响会被平滑。一个极端的日内价格波动,在平均价格计算中只占很小一部分,这使得亚式期权相对于传统期权具有更低的内在波动性。对于期权买方而言,这意味着降低了因单日异常价格波动而导致期权价值大幅下跌的风险;对于期权卖方而言,也降低了因极端价格事件而面临巨额赔付的风险。
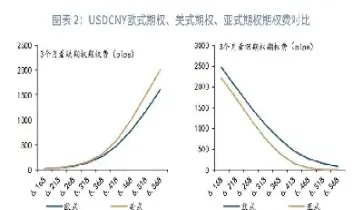
3. 期权费通常更低(Generally Cheaper Premium):由于平均价格的计算方式降低了期权支付的方差(variance),即期权到期价值的不确定性降低,因此亚式期权的期权费通常会比同等条件的欧式或美式期权更低。这使得它成为一种成本效益更高的风险管理工具,尤其适合那些预算有限但又需要长期对冲的机构或企业。
4. 有效规避价格操纵(Discourages Price Manipulation):由于亚式期权的支付不依赖于某个单一时刻的价格,试图通过操纵某一特定时间点的价格来影响期权价值的做法将变得极其困难且成本高昂。这增强了市场的公平性和稳定性。
5. 适用于长期套期保值(Suitable for Long-Term Hedging):对于那些其业务性质决定了需按平均价格进行结算或长期面临平均价格风险的企业(如大宗商品贸易商、制造商等),亚式期权是理想的套期保值工具。它能更好地匹配其内在的风险敞口,提供更精准的对冲效果。
3. 亚式期权的分类:平均价格与平均行权价
根据期权收益中“平均值”所扮演的角色,亚式期权进一步细分为两种主要类型:平均价格亚式期权和平均行权价亚式期权。
1. 平均价格亚式期权(Average Price Asian Option / Average Rate Option):
定义:这是一种固定行权价(Strike Price, K)的期权,但其支付是基于标的资产在观察期内的平均价格(Average Price, S_Avg)与固定行权价之间的差额来计算。
支付公式:
对于看涨期权(Call):`max(0, S_Avg - K)`
对于看跌期权(Put):`max(0, K - S_Avg)`
应用场景:这是最常见的亚式期权形式。它主要用于对冲在特定时期内其成本或收入与标的资产平均市场价格挂钩的风险。例如,一家石油公司可能需要对冲未来几个月内销售石油的平均价格风险,以确保其平均收入达到预设目标。
2. 平均行权价亚式期权(Average Strike Asian Option / Average Strike Rate Option):
定义:这种期权不是固定行权价,而是其行权价由标的资产在观察期内的平均价格(S_Avg)来确定,而期权的支付则由到期日标的资产的最终价格(S_T)与这个平均行权价之间的差额来计算。
支付公式:
对于看涨期权(Call):`max(0, S_T - S_Avg)`
对于看跌期权(Put):`max(0, S_Avg - S_T)`
应用场景:这种期权通常用于对冲不同市场价格或汇率之间的价差风险。例如,一家跨国公司可能需要对冲在未来一段时间内,其特定货币的平均买入价与其最终卖出价之间的不利波动,以确保交易的利润空间。它能有效帮助投资者以某种平均水平的价格进行买卖,从而降低因市场波动导致行权价不利的风险。
4. 平均方式与定价考量
在计算亚式期权的平均价格时,主要有两种方法:算术平均和几何平均。这两种平均方式不仅影响期权的最终支付,也对其定价过程带来了不同的复杂性。
1. 平均方式:
算术平均(Arithmetic Average):这是最直观和常见的平均方式,即将观察期内所有交易日(或特定观察点)的标的资产价格简单相加,然后除以观察点的数量。
公式:`S_Avg = (S1 + S2 + ... + Sn) / n`
特点:计算简单,更符合实际商业场景中对“平均成本”或“平均收入”的理解。
几何平均(Geometric Average):这种方式是将观察期内所有观察点的价格相乘,然后开n次方根(n为观察点数量)。
公式:`S_Avg = (S1 S2 ... Sn)^(1/n)`
特点:在数学上,几何平均值总是小于或等于算术平均值。它通常用于计算复合平均增长率,并在某些期权定价模型中具有更好的解析解特性。
2. 定价考量与复杂性:
算术平均亚式期权:由于标的资产价格通常被建模为服从对数正态分布,而多个对数正态变量之和不再是对数正态分布,这导致算术平均亚式期权通常没有简单的解析定价公式(如Black-Scholes模型)。其定价通常需要依赖更复杂的数值方法,如:
蒙特卡洛模拟(Monte Carlo Simulation):通过模拟大量标的资产价格路径,计算每条路径的平均价格和对应的期权支付,然后取平均得到期权估值。这是最常用且灵活的方法。
有限差分法(Finite Difference Method)或树形模型(Tree Models):在某些特定条件下也可以应用,但实现起来可能比传统欧式期权更复杂。
近似方法(Approximation Methods):例如,通过将算术平均近似为对数正态分布,可以推导出近似的Black-Scholes公式。
几何平均亚式期权:由于多个对数正态变量的乘积仍然服从对数正态分布,几何平均亚式期权在某些特定条件下可以推导出相对简单的解析定价公式,类似于Black-Scholes模型。这使得其定价在计算上更加高效和便捷。
定价的复杂性是亚式期权交易中一个重要的考虑因素。交易者和风险管理人员需要了解不同的平均方法如何影响期权价值,并选择合适的定价模型来准确评估这些衍生品的风险和回报。
亚式期权凭借其独特的平均价格结算机制,为金融市场提供了一种有效的风险管理工具。它不仅能显著降低短期市场波动带来的风险,还能以相对较低的成本实现长期的套期保值目标,尤其适合那些面临持续性平均价格风险的企业和投资者。无论是通过平均价格还是平均行权价的形式,亚式期权都提供了一种更为精细和灵活的方式来管理复杂的市场敞口。尽管其定价相比传统期权更为复杂,通常需要借助蒙特卡洛模拟等数值方法,但其在特定应用场景下的优越性,使其成为现代金融工程中不可或缺的一部分。理解亚式期权的各项名词和特性,对于深化对衍生品市场的认识,并有效运用这些工具进行风险管理和投资决策,都具有重要的意义。