期权定价模型度量什么的(期权定价模型分析)

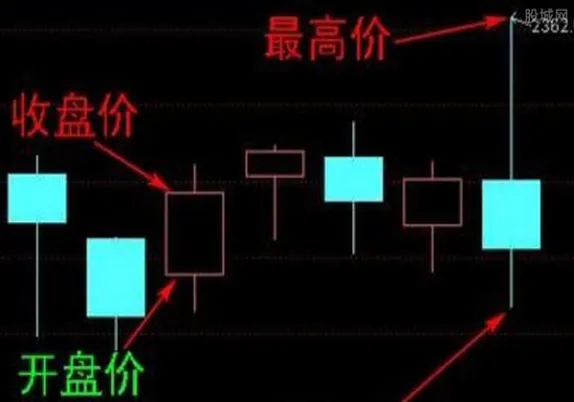
期权定价模型，顾名思义，是用于估算期权理论价值的数学模型。它的作用远不止于简单地计算一个数字。期权定价模型不仅能帮助投资者和交易员判断期权价格是否合理，更能深入分析潜在的风险和回报，并为复杂的投资策略提供理论基础。 简单来说，期权定价模型度量的是期权合约的理论价值，这个价值反映了标的资产未来价格波动的不确定性和时间价值。

期权定价模型的核心：风险中性定价

期权定价模型的核心思想是风险中性定价。 这种定价方法并非假设投资者是风险中性的，而是通过构建一个由标的资产和期权组成的无风险组合，从而将期权的价格与标的资产的价格联系起来。 换句话说，模型假设在风险中性的世界里，所有资产的预期收益率都等于无风险利率。 虽然现实世界并非如此，但这种假设简化了期权定价的计算过程，并能得出相对准确的结果。 风险中性定价的关键在于利用标的资产和期权之间的动态对冲关系，这意味着投资者可以不断调整组合的比例，以保持无风险状态。 这种动态对冲策略是期权定价模型的基础，也是期权交易中风险管理的重要手段。

Black-Scholes模型与Merton模型的应用

Black-Scholes模型和Merton模型是期权定价领域最经典的两个模型。Black-Scholes模型适用于欧式看涨期权和看跌期权的定价，它假设标的资产价格服从几何布朗运动，并考虑了标的资产价格、执行价格、无风险利率、剩余期限和波动率等因素。Merton模型则是在Black-Scholes模型的基础上，考虑了标的资产在期权到期前可能派发股息的情况，更适用于股票期权的定价。 这两个模型在实际应用中非常广泛，被用于期权交易、风险管理、投资组合构建等多个领域。 尽管它们存在一些局限性，例如假设波动率恒定、忽略交易成本等，但它们仍然是期权定价的基准，为后续模型的开发提供了重要的参考。

波动率：期权定价的关键参数

波动率是期权定价模型中最关键的参数之一，它反映了标的资产价格未来波动的程度。 波动率越高，期权的价格通常也越高，因为标的资产价格更有可能达到执行价格。 波动率可以分为历史波动率和隐含波动率。 历史波动率是基于过去一段时间的标的资产价格数据计算出来的，反映了过去的价格波动情况。 隐含波动率则是通过期权的市场价格反推出来的，反映了市场对未来波动率的预期。 交易员通常会利用隐含波动率来判断期权价格是否被高估或低估，并制定相应的交易策略。 隐含波动率也常被用于衡量市场情绪，例如，当市场出现恐慌时，隐含波动率通常会大幅上升。

期权定价模型在风险管理中的作用

期权定价模型不仅可以用于期权定价，还可以用于风险管理。 通过期权定价模型，我们可以计算出期权的Delta、Gamma、Vega、Theta和Rho等风险参数，这些参数反映了期权价格对标的资产价格、波动率、时间和利率等因素的敏感度。 利用这些风险参数，投资者可以更好地管理期权头寸的风险，例如，通过Delta对冲来降低标的资产价格波动带来的风险，或者通过Vega对冲来降低波动率变化带来的风险。 期权定价模型还可以用于计算VaR（Value at Risk）和压力测试，从而评估投资组合在极端情况下的潜在损失。 期权定价模型是风险管理的重要工具。

期权定价模型的局限性与改进

尽管期权定价模型在金融领域发挥着重要作用，但它们也存在一些局限性。 例如，Black-Scholes模型假设波动率恒定，但实际上波动率是会随时间变化的。 这些模型通常忽略了交易成本、流动性风险和跳跃风险等因素。 为了克服这些局限性，研究人员开发了许多改进的模型，例如，考虑波动率微笑和波动率曲面的模型，以及考虑跳跃过程的模型。 这些改进的模型更加复杂，但也能更准确地反映现实市场的特征。

期权定价模型与投资策略

期权定价模型可以为各种投资策略提供理论基础。 例如，利用期权定价模型可以判断期权价格是否被高估或低估，从而制定买入或卖出期权的策略。 期权定价模型还可以用于构建复杂的期权组合，例如，保护性看跌期权、备兑看涨期权、跨式期权和勒式期权等。 这些期权组合可以用于对冲风险、获取收益或表达对市场走势的看法。 例如，如果投资者预期市场波动率将上升，可以买入跨式期权或勒式期权，从波动率的上升中获利。 期权定价模型是制定投资策略的重要工具。