看跌期权价格公式(看跌期权价值计算公式)

在金融衍生品市场中，期权以其独特的非线性收益特性，成为对冲风险、锁定利润或进行投机的重要工具。其中，看跌期权（Put Option）赋予持有人在特定日期或之前以约定价格出售标的资产的权利而非义务。了解看跌期权的价值构成及定价机制，对于投资者和风险管理者而言至关重要。看跌期权的价格并非凭空产生，而是由一系列因素共同作用，并通过成熟的数学模型计算得出。将深入探讨看跌期权的价格公式，剖析其背后的经济学原理与数学逻辑，帮助读者全面理解看跌期权的价值计算方法。

看跌期权的价格反映了市场对其未来价值的预期。一个精确的定价模型不仅能为期权交易者提供参考，判断期权是否被高估或低估，还能帮助金融机构进行风险管理和产品设计。从最简单的内在价值和时间价值的界定，到复杂的Black-Scholes模型，看跌期权定价的演变是金融数学和量化分析发展的缩影。

看跌期权的核心概念

在深入探讨看跌期权的价格公式之前，我们首先需要理解看跌期权的基本构成和功能。看跌期权，简称“看跌”，是一种赋予其持有人在期权合约规定的到期日或之前（对于美式期权）或仅在到期日（对于欧式期权），以合约约定的执行价格（Strike Price）出售一定数量标的资产（Underlying Asset）的权利，而非义务的金融合约。购买看跌期权的投资者通常预期标的资产价格将下跌，以便在未来以高于市价的执行价格出售资产，从而获利。

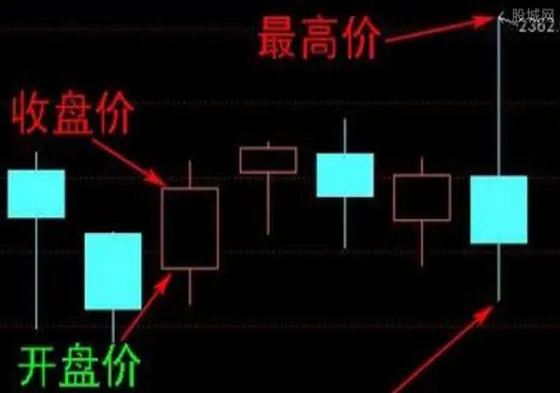
看跌期权具有双重价值：内在价值和时间价值。

• 内在价值（Intrinsic Value）：这是期权立即执行所能获得的收益。对于看跌期权而言，其内在价值为执行价格与当前标的资产价格之差（K - S）和零之间的较大值，即 Max(0, K - S)。当标的资产价格低于执行价格时，看跌期权具有内在价值，称之为“实值期权”（In-the-money）。反之，当标的资产价格高于执行价格时，看跌期权的内在价值为零，称之为“虚值期权”（Out-of-the-money）。当标的资产价格等于执行价格时，看跌期权处于“平值状态”（At-the-money）。
• 时间价值（Time Value）：这是期权价格扣除内在价值后的剩余部分。它反映了期权到期前标的资产价格朝有利方向变动的可能性。期权到期时间越长，标的资产价格波动的可能性越大，其时间价值通常也越高。随着到期日的临近，期权的时间价值会逐渐衰减，这一现象被称为“时间衰减”（Time Decay）。时间价值是期权定价中的关键组成部分，因为它包含了未来不确定性带来的溢价。

看跌期权的理论价格 = 内在价值 + 时间价值。

影响看跌期权价格的关键因素

看跌期权的价格并非由单一因素决定，而是由六个主要变量共同影响。理解这些因素如何作用是掌握定价公式的基础：

• 1. 标的资产当前价格 (S)：标的资产价格与看跌期权价格呈负相关。当标的资产价格下跌时，看跌期权变得更有价值，因为持有人可以在更高价格出售资产的权利变得更有利可图。
• 2. 执行价格 (K)：执行价格与看跌期权价格呈正相关。执行价格越高，看跌期权在未来以更高价格出售资产的机会越大，其价值也就越高。
• 3. 到期时间 (T)：到期时间与看跌期权价格通常呈正相关。到期时间越长，标的资产价格发生有利波动的可能性越大，看跌期权的时间价值越高。但需注意，时间价值的衰减速度并非线性，在临近到期时会加速。
• 4. 波动率 (σ)：波动率与看跌期权价格呈正相关。标的资产价格的波动性越大，其价格大幅下跌从而使看跌期权成为实值的可能性就越大，因此期权价值越高。
• 5. 无风险利率 (r)：无风险利率与看跌期权价格呈负相关。较高的无风险利率会降低未来执行价格的现值，从而略微降低看跌期权的价值。从另一角度看，如果投资者不购买期权，而是将资金投资于无风险资产，则会获得更高的收益，这使得持有期权的成本相对增加。
• 6. 股息率 (q)：对于会派发股息的股票期权，股息率与看跌期权价格呈正相关。当标的资产派发股息时，其价格会在除息日下跌，这对看跌期权持有人有利，因为标的资产价格下跌会增加看跌期权的内在价值，或者说使其更有可能成为实值。预期股息越高，看跌期权的价值越高。对于不派发股息的资产，此项为零。

Black-Scholes看跌期权定价模型

Black-Scholes模型是金融工程领域最具里程碑意义的成果之一，它提供了一个计算欧式期权（包括看跌期权和看涨期权）理论价格的数学公式。该模型基于一系列严格的假设，例如市场有效、股价服从对数正态分布、无交易成本、无套利机会、无风险利率和波动率恒定等。尽管这些假设在现实中难以完全满足，但Black-Scholes模型因其简洁和实用性，至今仍是期权定价和风险管理的基础工具。

Black-Scholes模型中看跌期权的价格（P）计算公式如下：

\[ P = K e^{-rT} N(-d_2) - S e^{-qT} N(-d_1) \]

其中：

• P：看跌期权的价格。
• K：