期权定价模型简述(期权定价模型主要有两种分别为)
期权,作为一种重要的金融衍生品,赋予持有者在未来特定日期或之前以约定价格买入或卖出标的资产的权利,而非义务。其独特的非线性收益特性,使得对期权进行合理定价成为金融市场中的核心挑战与研究热点。一个准确的期权定价模型不仅能帮助投资者进行风险管理、套期保值,还能为市场提供重要的价格发现功能,从而促进资源的有效配置。在众多期权定价模型中,有两大模型因其深远的影响力和广泛的应用而被称为基石:布莱克-斯科尔斯(Black-Scholes)模型和二叉树(Binomial Tree)模型。它们分别从连续时间和离散时间两个维度,为期权定价提供了强大的理论框架和实用工具。将深入探讨这两种模型的核心思想、假设、优缺点及其适用场景。
期权定价的核心挑战与意义
期权定价的复杂性源于其价值受到多种动态因素的影响。这些因素包括标的资产当前价格、行权价格、到期时间、无风险利率、标的资产价格波动率以及潜在的股息支付等。其中,波动率尤其难以准确预测,因为它反映了市场对未来价格变动幅度的预期,具有高度不确定性。期权价值的非线性特征意味着其对这些变量变化的敏感度并非恒定,这进一步增加了定价的难度。
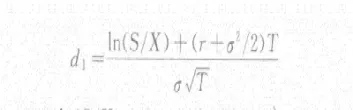
尽管存在挑战,准确的期权定价对于金融市场具有极其重要的意义。它为投资者提供了一个衡量期权公允价值的基准,有助于识别被高估或低估的期权,从而进行套利或投机交易。对于需要对冲风险的企业和个人而言,期权定价模型能够帮助他们计算出实现所需风险管理目标的期权组合成本。例如,通过购买看跌期权来对冲股票下跌风险,其成本的合理性判断就离不开定价模型。期权定价模型是构建更复杂金融产品和进行风险分析的基础。例如,期权敏感性指标(如Delta、Gamma、Vega等,统称为“希腊字母”)的计算,就直接来源于定价模型,这些指标对于量化和管理期权头寸的风险至关重要。期权定价模型也促进了金融创新,为结构化产品和复杂衍生品的开发提供了理论支撑。
二叉树期权定价模型:直观与灵活
二叉树期权定价模型,由考克斯(Cox)、罗斯(Ross)和鲁宾斯坦(Rubinstein)于1979年提出,通常被称为CRR模型。它是一种离散时间模型,其核心思想是将标的资产价格在期权有效期内的变动路径简化为一系列离散的向上或向下运动。模型将期权有效期划分为N个小时间步长,在每个步长结束时,标的资产价格要么上升到某一固定比例,要么下降到另一固定比例。通过这种方式,可以构建一个树状结构,描绘出标的资产价格在到期日所有可能的最终状态。
二叉树模型的关键在于“无套利”原理和“风险中性定价”概念。在每个节点,模型通过构建一个由标的资产和无风险债券组成的复制组合,使其在下一个时间点与期权的支付完全匹配。由于这个复制组合与期权具有相同的未来现金流,且不存在套利机会,因此期权在当前时点的价值就等于该复制组合的成本。通过从期权到期日开始,逆向推导(即“回溯归纳法”)至当前时点,就可以得到期权的现值。在推导过程中,会使用到风险中性概率,即假设投资者对风险是中性的,预期收益率等于无风险利率。
二叉树模型的优势在于其直观性和灵活性。它能够清晰地描绘出标的资产价格的演变路径,使得定价过程易于理解。更重要的是,二叉树模型能够自然地处理美式期权(允许在到期日之前任何时间行权)的定价问题。通过在每个节点比较立即行权价值与继续持有期权的价值,选择两者中较大者作为期权在该节点的价值,从而捕捉美式期权的早期行权特征。它还能方便地处理股息支付、分红、复杂的行权条件等非标准特征。二叉树模型的缺点是,当时间步长N较大时,计算量会显著增加,且其离散化的假设与实际市场连续波动的特性存在一定差异。
布莱克-斯科尔斯模型:连续时间的里程碑
布莱克-斯科尔斯(Black-Scholes)模型,由费舍尔·布莱克(Fischer Black)和迈伦·斯科尔斯(Myron Scholes)于1973年提出,并由罗伯特·默顿(Robert Merton)进一步完善,为期权定价领域带来了革命性的突破。该模型基于连续时间框架,假设标的资产价格服从几何布朗运动,且市场是无摩擦的(无交易成本、无税收、可以无限制地借贷和卖空)。它提供了一个封闭形式(即有明确数学公式)的欧式期权(只能在到期日行权)定价公式。
布莱克-斯科尔斯模型的核心假设包括:
- 标的资产价格服从对数正态分布(即其收益率服从正态分布)。
- 无风险利率和波动率在期权有效期内是常数。
- 期权是欧式期权,不能提前行权。
- 标的资产在期权有效期内不支付股息。
- 市场无摩擦,不存在套利机会,且可以连续交易。
在这些假设下,布莱克和斯科尔斯通过构建一个动态调整的无风险对冲组合(由标的资产和期权组成),并利用偏微分方程推导出了期权的定价公式。该公式的输入包括:标的资产当前价格、行权价格、到期时间、无风险利率和标的资产价格波动率。其输出是一个精确的理论期权价格。
布莱克-斯科尔斯模型的优点在于其简洁、高效和优雅。它提供了一个易于计算的解析解,成为金融市场上最广泛使用的期权定价工具。该模型不仅能计算期权价格,还能通过对公式求偏导,得出期权的敏感性指标(“希腊字母”),如Delta(衡量期权价格对标的资产价格变化的敏感度)、Gamma(衡量Delta对标的资产价格变化的敏感度)、Vega(衡量期权价格对波动率变化的敏感度)和Theta(衡量期权价格对时间流逝的敏感度),这些指标对于期权风险管理至关重要。布莱克-斯科尔斯模型的缺点也显而易见,其严格的假设条件在现实市场中往往难以完全满足。例如,波动率通常并非恒定,而是随时间变化或随行权价变化(即“波动率微笑”现象);提前行权的美式期权也无法直接用此模型定价;股息支付也会影响模型准确性。
两大模型对比与适用场景
布莱克-斯科尔斯模型和二叉树模型虽然都旨在解决期权定价问题,但它们在理论基础、适用范围和计算特性上存在显著差异:
- 时间处理方式:布莱克-斯科尔斯模型是连续时间模型,假设标的资产价格连续变动;而二叉树模型是离散时间模型,将期权有效期划分为有限的步长。