期权一个点是多少(期权的价格是怎么算的)

期权交易中，“一点”的含义以及期权价格的计算方式，对于理解期权交易至关重要，也是许多新手投资者感到困惑的地方。将详细解释“一点”的含义，并深入探讨期权价格的计算方法及影响因素。

我们需要明确一点：期权的“一点”指的是期权价格的最小变动单位，而不是标的资产的价格变动单位。 期权合约的价格通常以最小变动单位（tick size）为增量进行报价，这个最小变动单位就叫做“一点”。 不同期权合约的“一点”大小各不相同，它取决于标的资产的价格和合约的乘数。例如，一个股指期权合约的“一点”可能代表0.1元，而一个个股期权合约的“一点”可能代表0.01元。 理解这一点至关重要，因为它直接关系到你的盈亏计算。如果一个期权价格上涨了一点，你的盈亏将根据你的持仓数量和一点的价值而定。

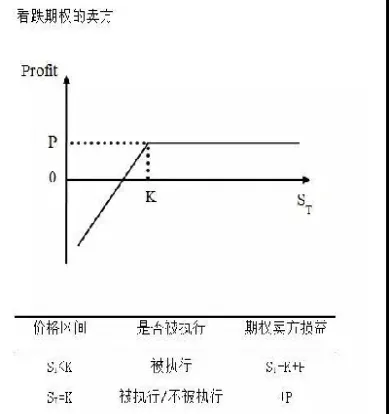
期权合约的乘数

期权合约的乘数决定了每一点价格变动对你的实际盈亏影响有多大。例如，一个股指期权合约的乘数通常为100，这意味着每一点的价格变动将导致你的盈亏变化100倍。如果一点价值为0.1元，那么期权价格上涨一点，你的盈亏将变化10元（0.1元/点 100）。而如果你的持仓数量为10张合约，那么你的盈亏将变化100元（10元/张 10张）。 所以，在计算盈亏时，必须考虑合约的乘数。

影响期权价格的因素：Black-Scholes模型

期权价格并非随意设定，而是由多种因素共同决定，其中最常用的定价模型是Black-Scholes模型 (布莱克-斯科尔斯模型)。这个模型考虑了以下几个关键因素：标的资产价格(S)、执行价格(K)、到期时间(T)、无风险利率(r)、波动率(σ)以及股息收益率(q)。

Black-Scholes模型是一个复杂的数学公式，但我们可以理解其核心思想：标的资产价格越高，期权价值越高（对于看涨期权）；执行价格越低，看涨期权价值越高；到期时间越长，期权价值越高；无风险利率越高，看涨期权价值越高；波动率越高，期权价值越高；股息收益率越高，看涨期权价值越低。对于看跌期权，这些关系则相反。

需要注意的是，Black-Scholes模型基于一些假设，例如市场是有效的、无摩擦的，以及波动率是恒定的。在实际市场中，这些假设往往难以完全满足，因此Black-Scholes模型计算出的价格只是一个理论价格，实际市场价格会存在一定的偏差。

期权价格的内在价值和时间价值

期权价格由两部分组成：内在价值和时间价值。

内在价值是指期权合约目前拥有的价值。对于看涨期权，内在价值等于标的资产价格减去执行价格（如果结果为正数，否则为0）。对于看跌期权，内在价值等于执行价格减去标的资产价格（如果结果为正数，否则为0）。

时间价值是指期权到期前剩余的时间所带来的价值。时间价值随着到期日的临近而逐渐减少，最终在到期日归零。时间价值受到波动率的影响较大，波动率越高，时间价值越高。

期权价格 = 内在价值 + 时间价值

波动率对期权价格的影响

波动率是影响期权价格最重要的因素之一。波动率是指标的资产价格在未来一段时间内的波动程度，通常用标准差来衡量。波动率越高，意味着标的资产价格未来可能出现更大的涨跌幅度，这增加了期权的潜在收益和风险，因此期权价格也越高。反之，波动率越低，期权价格越低。

投资者可以通过观察市场上的隐含波动率来判断市场对未来价格波动的预期。隐含波动率是市场上期权价格所反映出的预期波动率，它通常会反映市场情绪和预期。

实际期权价格的获取

虽然Black-Scholes模型提供了期权价格的理论计算方法，但实际交易中，投资者通常不会自己计算期权价格。期权交易平台会根据市场供求关系和各种定价模型实时更新期权价格，投资者可以直接从交易平台上获取期权的实时报价，包括买卖价差、最后交易价等信息。这些价格已经综合考虑了各种影响因素，包括Black-Scholes模型、市场供求关系、交易成本等。

理解期权“一点”的含义和影响期权价格的因素，对于投资者进行有效的风险管理和制定合理的交易策略至关重要。 投资者应该结合自身的风险承受能力和市场情况，谨慎进行期权交易。

总而言之，“一点”是期权价格的最小变动单位，其具体数值取决于合约乘数和标的资产的特性。期权价格的计算是一个复杂的过程，受多种因素影响，Black-Scholes模型提供了一个理论框架，但实际价格由市场供求决定。 投资者需要充分理解这些因素才能更好地进行期权交易。