bs期权定价公式的前提(bs期权定价模型的参数)
Black-Scholes期权定价模型(简称BS模型)是金融学中一个里程碑式的成果,它为欧式期权的定价提供了一个简洁而优雅的公式。这个公式的推导和应用都依赖于一系列严苛的前提假设,这些假设决定了模型的适用范围和局限性。理解这些前提条件对于正确理解和应用BS模型至关重要,否则可能会导致严重的定价误差和风险管理失误。将详细阐述BS期权定价公式的前提条件,即BS模型的参数,并分析其对模型的影响。
1. 标的资产价格服从几何布朗运动
BS模型的核心假设是标的资产价格(例如股票价格)遵循几何布朗运动(Geometric Brownian Motion,GBM)。GBM是一种随机过程,其对数收益率服从正态分布。这意味着在任意给定的时间段内,标的资产价格的相对变化率服从正态分布,其均值和方差与时间成正比。具体来说,假设标的资产价格为S,则其在时间t的微小变化dS可以表示为:
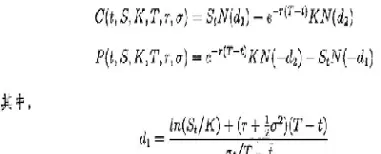
dS = μSdt + σSdz
其中,μ代表标的资产的预期收益率(漂移率),σ代表标的资产价格波动率,dt代表时间增量,dz是维纳过程(标准布朗运动)的增量,它代表随机因素的影响。这个公式表明,标的资产价格的变化由一个确定性部分(μSdt)和一个随机部分(σSdz)组成。GBM假设保证了价格变化的连续性和随机性,这为BS模型的数学推导提供了基础。实际市场中资产价格的波动往往表现出非正态分布的特征,例如尖峰厚尾现象(fat tails),这使得BS模型在某些情况下无法准确反映实际情况。
2. 无风险利率恒定且已知
BS模型假设存在一个无风险利率r,它在期权有效期内保持恒定且已知。这意味着投资者可以以无风险利率借入或贷出资金。这个假设简化了模型的计算,但实际市场中利率是不断变化的,且存在各种期限的利率曲线。BS模型在利率变化频繁的情况下可能产生偏差。为了弥补这个缺陷,一些改进的模型引入了随机利率或使用期限结构模型来处理利率的变动。
3. 期权为欧式期权
BS模型只适用于欧式期权,即只有在期权到期日才能行权的期权。美式期权(可以在到期日之前任何时间行权)的定价更为复杂,因为需要考虑提前行权的可能性,而BS模型无法处理这种可能性。对于美式期权的定价,需要采用更复杂的数值方法,例如二叉树模型或有限差分法。
4. 没有交易成本和税收
BS模型假设市场是完全有效的,这意味着没有交易成本和税收。在实际市场中,交易成本和税收会对投资者的决策产生影响,进而影响期权的定价。忽略这些因素会使BS模型的结果与实际情况存在偏差。尤其是在高频交易中,交易成本的影响不容忽视。
5. 标的资产不支付股息
最初的BS模型假设标的资产不支付股息。如果标的资产支付股息,则需要对模型进行修正。股息会降低标的资产的价格,从而影响期权的价值。通常,在修正后的模型中,需要考虑股息的现值,并将它从标的资产价格中扣除。
6. 市场是完全有效的
BS模型隐含地假设了市场是完全有效的。这意味着市场信息是完全公开透明的,所有投资者都能以相同的价格买卖标的资产,并且没有套利机会。在实际市场中,信息不对称、市场摩擦以及操纵行为的存在都会导致市场效率的降低,从而影响BS模型的准确性。完全有效市场的假设保证了套利交易能够迅速消除任何价格差异,这是BS模型推导的核心逻辑之一。
总而言之,Black-Scholes期权定价模型的适用性依赖于一系列理想化的假设。虽然这些假设在现实世界中往往难以完全满足,但BS模型仍然是一个重要的定价工具,它为理解期权定价提供了基础框架。在实际应用中,需要根据具体的市场情况对模型进行调整或选择更复杂的模型,以提高定价的准确性。同时,我们也需要充分认识到BS模型的局限性,避免盲目依赖和过度应用。